读者会不会觉得一元线性回归模型比较简单呢？它反映的是单个自变量对因变量的影响，然而实际情况中，影响因变量的自变量往往不止一个，从而需要将一元线性回归模型扩展到多元线性回归模型。

如果构建多元线性回归模型的数据集包含n个观测、p+1个变量（其中p个自变量和1个因变量），则这些数据可以写成下方的矩阵形式：

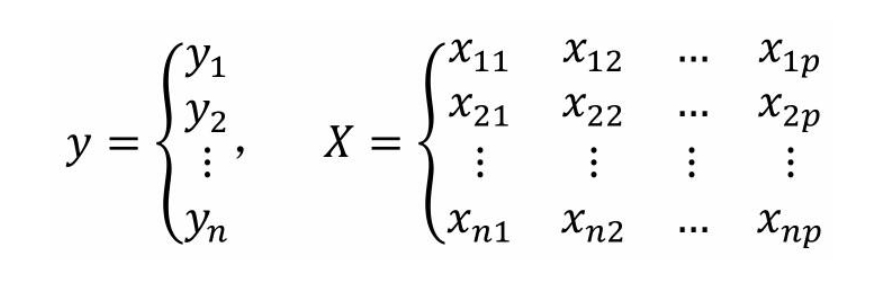
其中，xij代表第个i行的第j个变量值。如果按照一元线性回归模型的逻辑，那么多元线性回归模型应该就是因变量y与自变量X的线性组合，即可以将多元线性回归模型表示成：

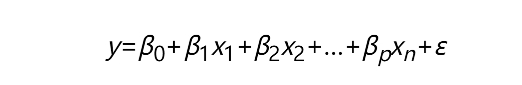
根据线性代数的知识，可以将上式表示成y=Xβ+ε。其中，β为p×1的一维向量，代表了多元线性回归模型的偏回归系数；ε为n×1的一维向量，代表了模型拟合后每一个样本的误差项。

7.2.1　回归模型的参数求解

在多元线性回归模型所涉及的数据中，因变量y是一维向量，而自变量X为二维矩阵，所以对于参数的求解不像一元线性回归模型那样简单，但求解的思路是完全一致的。为了使读者掌握多元线性回归模型参数的求解过程，这里把详细的推导步骤罗列到下方：

第一步：构建目标函数

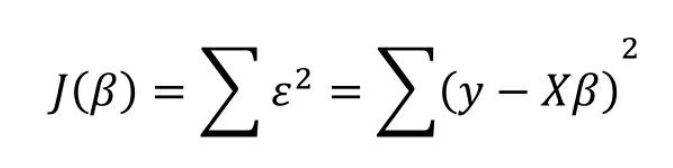
根据线性代数的知识，可以将向量的平方和公式转换为向量的内积，接下来需要对该式进行平方项的展现。

第二步：展开平方项

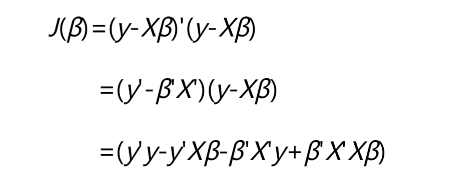
由于上式中的y’Xβ和β’X’y均为常数，并且常数的转置就是其本身，因此y’Xβ和β’X’y是相等的。接下来，对目标函数求参数β的偏导数。

第三步：求偏导

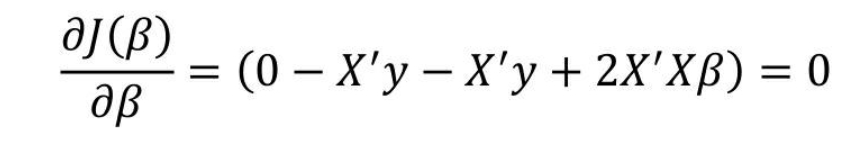
如上式所示，根据高等数学的知识可知，欲求目标函数的极值，一般都需要对目标函数求导数，再令导函数为0，进而根据等式求得导函数中的参数值。

第四步：计算偏回归系数的值

经过如上四步的推导，最终可以得到偏回归系数β与自变量X、因变量y的数学关系。这个求解过程也被成为“最小二乘法”。基于已知的偏回归系数β就可以构造多元线性回归模型。前文也提到，构建模型的最终目的是为了预测，即根据其他已知的自变量X的值预测未知的因变量y的值。

7.2.2　回归模型的预测

如果已经得知某个多元线性回归模型y=β0+β1x1+β2x2+…+βpxn，当有其他新的自变量值时，就可以将这些值带入如上的公式中，最终得到未知的y值。在Python中，实现线性回归模型的预测可以使用predict“方法”，关于该“方法”的参数含义如下：

    predict(exog=None, transform=True)

exog：指定用于预测的其他自变量的值。
transform：bool类型参数，预测时是否将原始数据按照模型表达式进行转换，默认为True。

接下来将基于statsmodels模块对多元线性回归模型的参数进行求解，进而依据其他新的自变量值实现模型的预测功能。这里不妨以某产品的利润数据集为例，该数据集包含5个变量，分别是产品的研发成本、管理成本、市场营销成本、销售市场和销售利润，数据集的部分截图如表7-1所示。

表7-1中数据集中的Profit变量为因变量，其他变量将作为模型的自变量。需要注意的是，数据集中的State变量为字符型的离散变量，是无法直接带入模型进行计算的，所以建模时需要对该变量进行特殊处理。有关产品利润的建模和预测过程如下代码所示：

如上结果所示，得到多元线性回归模型的回归系数及测试集上的预测值，为了比较，将预测值和测试集中的真实Profit值罗列在一起。针对如上代码需要说明三点：

为了建模和预测，将数据集拆分为两部分，分别是训练集（占80%）和测试集（占20%），训练集用于建模，测试集用于模型的预测。

由于数据集中的State变量为非数值的离散变量，故建模时必须将其设置为哑变量的效果，实现方式很简单，将该变量套在C()中，表示将其当作分类（Category）变量处理。

对于predict“方法”来说，输入的自变量X与建模时的自变量X必须保持结构一致，即变量名和变量类型必须都相同，这就是为什么代码中需要将test数据集的Profit变量删除的原因。

对于输出的回归系数结果，读者可能会感到疑惑，为什么字符型变量State对应两个回归系数，而且标注了Florida和New York。那是因为字符型变量State含有三种不同的值，分别是California、Florida和New York，在建模时将该变量当作哑变量处理，所以三种不同的值就会衍生出两个变量，分别是State[Florida]和State[New York]，而另一个变量State[California]就成了对照组。

正如建模中的代码所示，将State变量套在C()中，就表示State变量需要进行哑变量处理。但是这样做会存在一个缺陷，那就是无法指定变量中的某个值作为对照组，正如模型结果中默认将State变量的California值作为对照组（因为该值在三个值中的字母顺序是第一个）。如需解决这个缺陷，就要通过pandas模块中的get_dummies函数生成哑变量，然后将所需的对照组对应的哑变量删除即可。为了使读者明白该解决方案，这里不妨重新建模，并以State变量中的New York值作为对照组，代码如下：

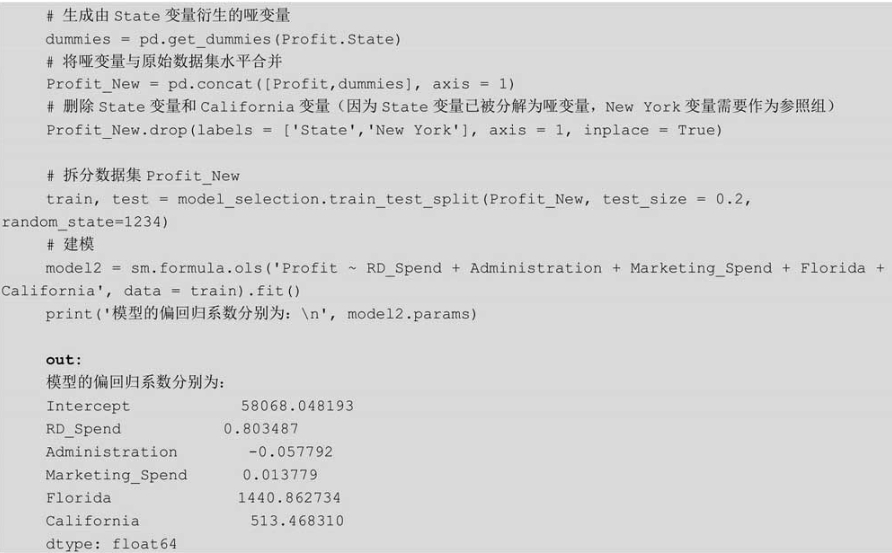
如上结果所示，从离散变量State中衍生出来的哑变量在回归系数的结果里只保留了Florida和California，而New York变量则作为了参照组。以该模型结果为例，得到的模型公式可以表达为：

Profit=58068.05+0.80RD_Spend-0.06Administation+0.01Marketing_Spend+1440.86Florida+513.47California

虽然模型的回归系数求解出来了，但从统计学的角度该如何解释模型中的每个回归系数呢？下面分别以研发成本RD_Spend变量和哑变量Florida为例，解释这两个变量对模型的作用：在其他变量不变的情况下，研发成本每增加1美元，利润会增加0.80美元；在其他变量不变的情况下，以New York为基准线，如果在Florida销售产品，利润会增加1440.86美元。

关于产品利润的多元线性回归模型已经构建完成，但是该模型的好与坏并没有相应的结论，还需要进行模型的显著性检验和回归系数的显著性检验。在下一节，将重点介绍有关线性回归模型中的几点重要假设检验。