一元线性回归模型也被称为简单线性回归模型,是指模型中只含有一个自变量和一个因变量,用来建模的数据集可以表示成{(x1,y1),(x2,y2),…,(xn,yn)}。其中,xi表示自变量x的第i个值,yi表示因变量y的第i个值,n表示数据集的样本量。当模型构建好之后,就可以根据其他自变量x的值,预测因变量y的值,该模型的数学公式可以表示成:
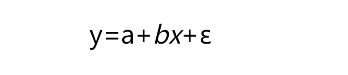
如上公式所示,该模型特别像初中所学的一次函数。其中,a为模型的截距项,b为模型的斜率项,ε为模型的误差项。模型中的a和b统称为回归系数,误差项ε的存在主要是为了平衡等号两边的值,通常被称为模型无法解释的部分。
为了使读者理解简单线性回归模型的数学公式,这里不妨以收入数据集为例,探究工作年限与收入之间的关系。在第6章的数据可视化部分已经介绍了有关散点图的绘制,下面将绘制工作年限与收入的散点图,并根据散点图添加一条拟合线:
# 导入第三方模块 import pandas as pd import matplotlib.pyplot as plt import seaborn as sns # 导入数据集 income = pd.read_csv(r'C:\Users\Administrator\Desktop\Salary_Data.csv') # 绘制散点图 sns.lmplot(x = 'YearsExperience', y = 'Salary', data = income, ci = None) # 显示图形 plt.show()
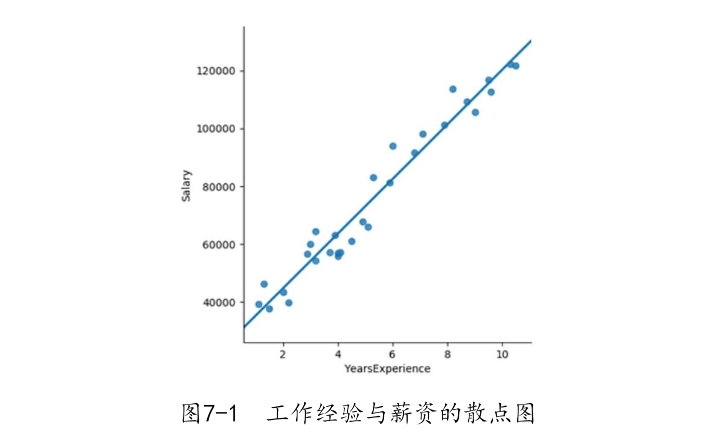
图7-1反映的就是自变量YearsExperience与因变量Salary之间的散点图,从散点图的趋势来看,工作年限与收入之间存在明显的正相关关系,即工作年限越长,收入水平越高。图中的直线就是关于散点的线性回归拟合线,从图中可知,每个散点基本上都是围绕在拟合线附近。虽然通过可视化的方法可以得知散点间的关系和拟合线,但如何得到这条拟合线的数学表达式呢?
拟合线的求解
本节的内容就是关于简单线性回归模型的求解,即如何根据自变量x和因变量y,求解回归系数a和b。前面已经提到,误差项ε是为了平衡等号两边的值,如果拟合线能够精确地捕捉到每一个点(所有的散点全部落在拟合线上),那么对应的误差项ε应该为0。按照这个思路来看,要想得到理想的拟合线,就必须使误差项ε达到最小。由于误差项是y与a+bx的差,结果可能为正值或负值,因此误差项ε达到最小的问题需转换为误差平方和最小的问题(最小二乘法的思路)。误差平方和的公式可以表示为:
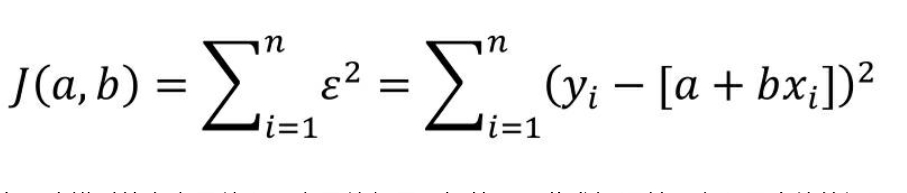
由于建模时的自变量值和因变量值都是已知的,因此求解误差平方和最小值的问题就是求解函数J(a,b)的最小值,而该函数的参数就是回归系数a和b。
该目标函数其实就是一个二元二次函数,如需使得目标函数J(a,b)达到最小,可以使用偏导数的方法求解出参数a和b,进而得到目标函数的最小值。关于目标函数的求导过程如下:
第一步:展开平方项
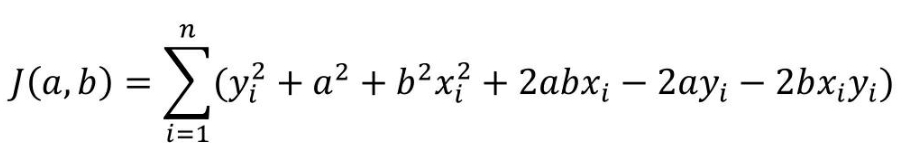
第二步:设偏导数为0
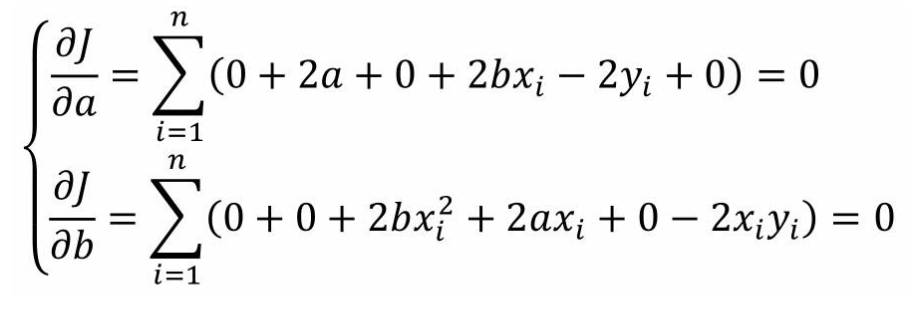
第三步:和公式转换

第四步:化解
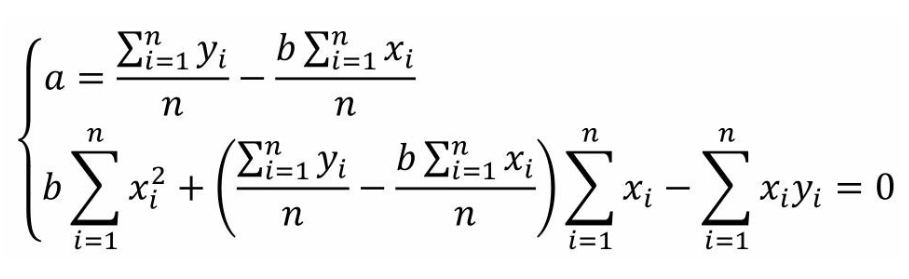
第五步:将参数a带入,求解b
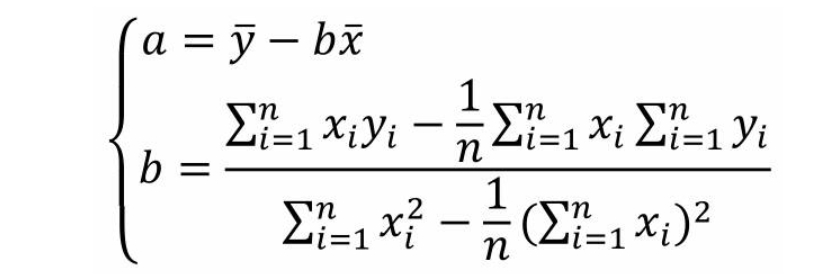
如上推导结果所示,参数a和b的值都是关于自变量x和因变量y的公式。接下来,根据该公式,利用Pyhton计算出回归模型的参数值a和b。

如上所示,利用Python的计算功能,最终得到模型的回归参数值。你可能会觉得麻烦,为了计算回归模型的参数还得人工写代码,是否有现成的第三方模块可以直接调用呢?答案是肯定的,这个模块就是statsmodels,它是专门用于统计建模的第三方模块,如需实现线性回归模型的参数求解,可以调用子模块中的ols函数。有关该函数的语法及参数含义可见下方:
ols(formula, data, subset=None, drop_cols=None)

这是一个语法非常简单的函数,而且参数也通俗易懂,但该函数的功能却很强大,不仅可以计算模型的参数,还可以对模型的参数和模型本身做显著性检验、计算模型的决定系数等。接下来,利用该函数计算模型的参数值,进而验证手工方式计算的参数是否正确:
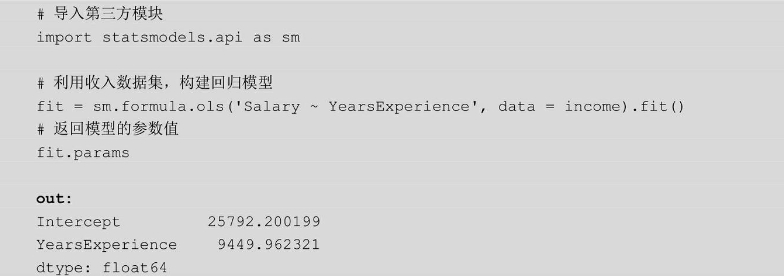
如上结果所示,Intercept表示截距项对应的参数值,YearsExperience表示自变量工作年限对应的参数值。对比发现,函数计算出来的参数值与手工计算的结果完全一致,所以,关于收入的简单线性回归模型可以表示成:
