此前，我们曾表示，虽然一些计算机拥有大量的电子计算元件、巨大的存储空间，并且这些计算机的运行频率比肉蓬蓬、软绵绵的生物大脑要快得多，但是即使是像鸽子一样小的大脑，其能力也远远大于这些电子计算机，这使得科学家们对动物的大脑迷惑不解。

请读者将注意力转向架构的不同。传统的计算机按照严格的串行顺序，相当准确具体地处理数据。对于这些冰冷坚硬的计算机而言，不存在模糊性或不确定性。而另一方面，动物的大脑表面上看起来以慢得多的节奏运行，却似乎以并行方式处理信号，模糊性是其计算的一种特征。

让我们来观察生物大脑中的基本单元—神经元。

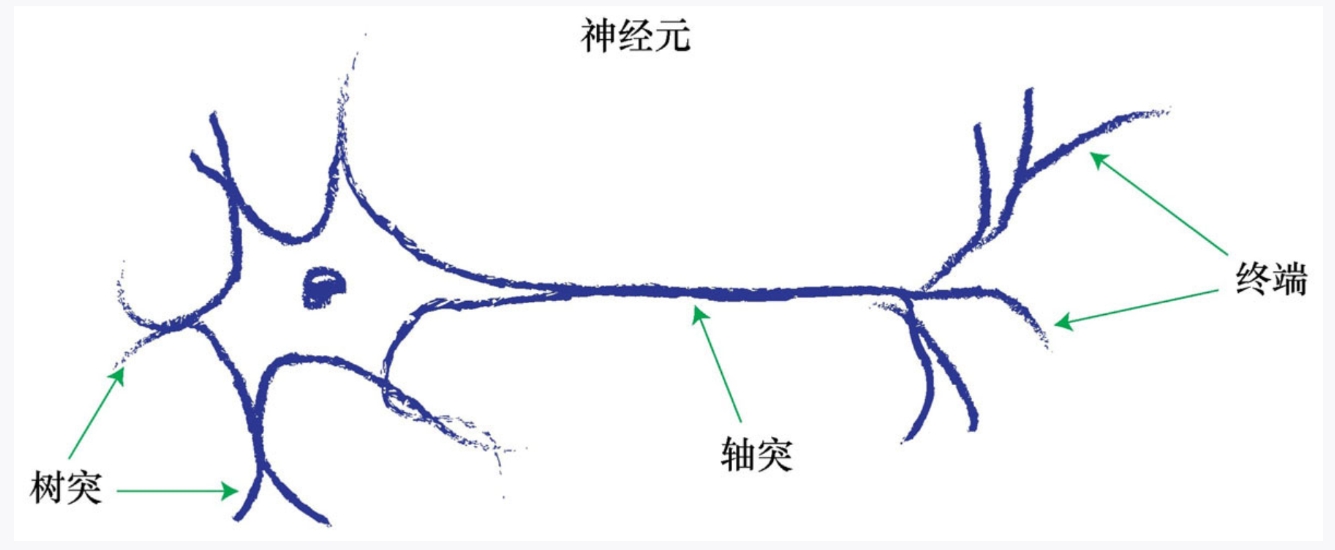
虽然神经元有各种形式，但是所有的神经元都是将电信号从一端传输到另一端，沿着轴突，将电信号从树突传到树突。然后，这些信号从一个神经元传递到另一个神经元。这就是身体感知光、声、触压、热等信号的机制。来自专门的感觉神经元的信号沿着神经系统，传输到大脑，而大脑本身主要也是由神经元构成的。

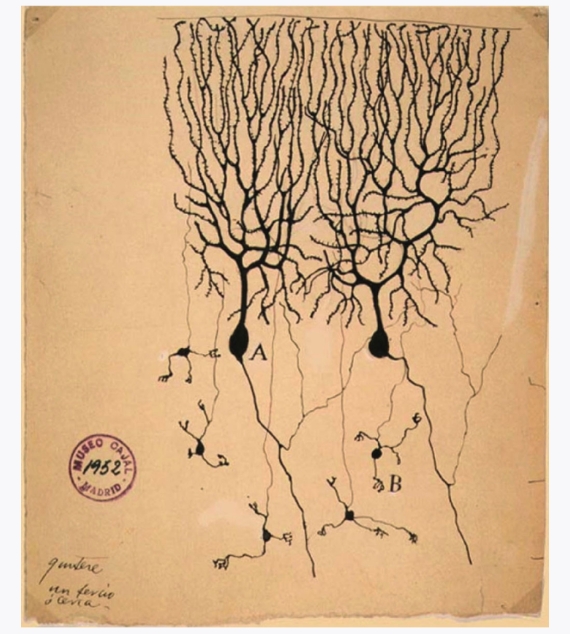
下面是由西班牙神经学家在1899年绘制的鸽子大脑的神经元草图。你可以看到关键部件—树突和终端。

我们需要多少个神经元才能执行相对复杂的有趣任务呢？

一般说来，能力非常强的人类大脑有大约1000亿个神经元！一只果蝇拥有约10万个神经元，能够飞翔、觅食、躲避危险、寻找食物以及执行许多相当复杂的任务。10万个神经元，这个数字恰好落在了现代计算机试图复制的范围内。一只线虫仅仅具有302个神经元，与今天的数字计算机资源相比，简直就是微乎其微！但是一只线虫能够完成一些相当有用的任务，而这任务对于尺寸大得多的传统计算机程序而言却难以完成。

那么，其中有什么秘密吗？生物的大脑要慢得多，并且比起现代计算机，其计算元件相对较少，但是为什么生物的大脑却有如此能力呢？大脑的全部功能（例如意识）仍是一个谜，但是关于神经元能够使用不同方式进行计算，也就是不同的求解问题的方式，人类掌握的知识已经足够我们使用了。

因此，我们来看看一个神经元是如何工作的。它接受了一个电输入，输出另一个电信号。这看起来，与我们先前所观察的分类或预测的机器一模一样，这些机器也是接受了一个输入，进行一些处理，然后弹出一个输出。

因此，我们可以与以前一样，将神经元表示为线性函数吗？虽然这是个好主意，但是不可以这样做。生物神经元与简单的线性函数不一样，不能简单地对输入做出的响应，生成输出。也就是说，它的输出不能采用这种形式：输出=（常数*输入）+（也许另一常数）。

观察表明，神经元不会立即反应，而是会抑制输入，直到输入增强，强大到可以触发输出。你可以这样认为，在产生输出之前，输入必须到达一个阈值。就像水在杯中—直到水装满了杯子，才可能溢出。直观上，这是有道理的—神经元不希望传递微小的噪声信号，而只是传递有意识的明显信号。下图说明了这种思想，只有输入超过了阈值（threshold），足够接通电路，才会产生输出信号。

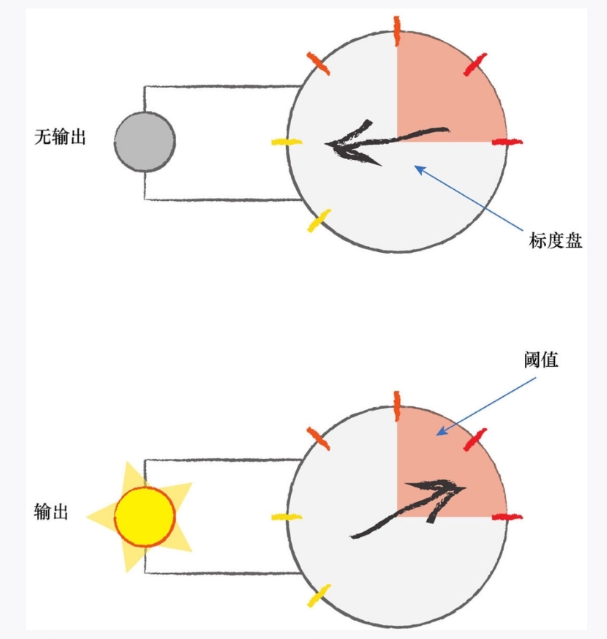
虽然这个函数接受了输入信号，产生了输出信号，但是我们要将某种称为激活函数的阈值考虑在内。在数学上，有许多激活函数可以达到这样的效果。一个简单的阶跃函数可以实现这种效果。

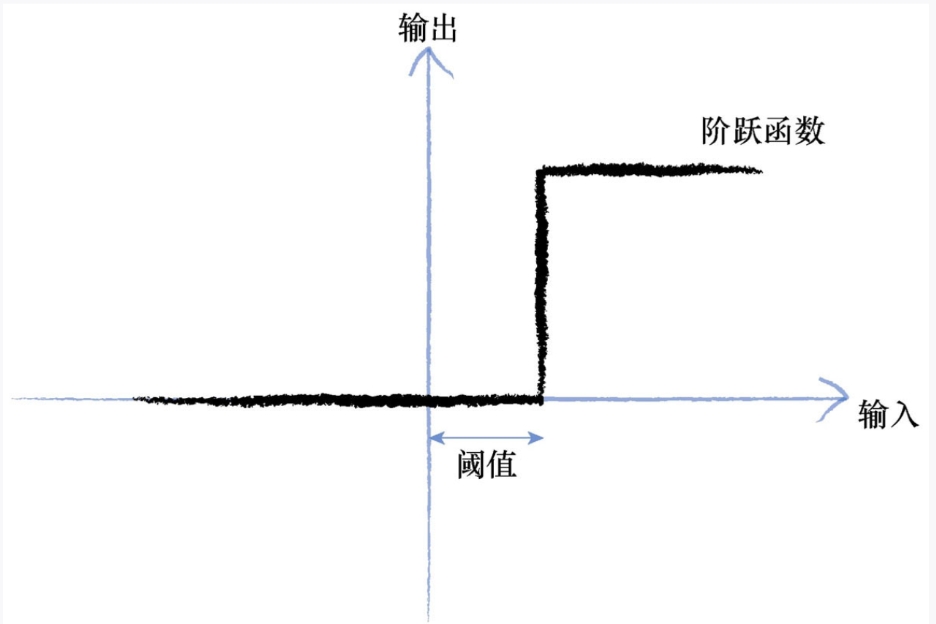
你可以看到，在输入值较小的情况下，输出为零。然而，一旦输入达到阈值，输出就一跃而起。具有这种行为的人工神经元就像一个真正的生物神经元。科学家所使用的术语实际上非常形象地描述了这种行为，他们说，输入达到阈值时，神经元就激发了。

我们可以改进阶跃函数。下图所示的S形函数称为S函数（sigmoid function）。这个函数，比起冷冰冰、硬邦邦的阶跃函数要相对平滑，这使得这个函数更自然、更接近现实。自然界很少有冰冷尖锐的边缘！

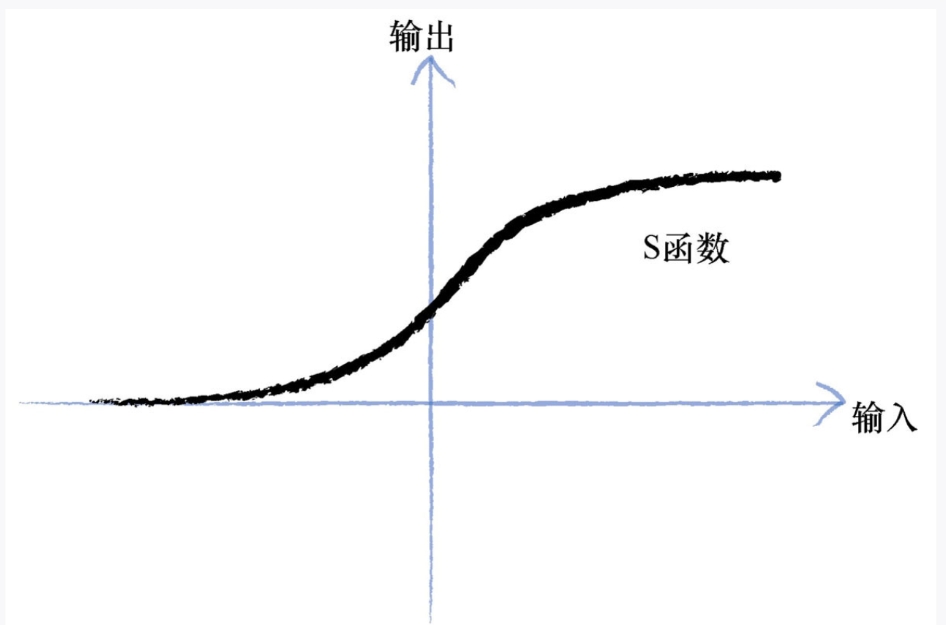
我们将继续使用这种平滑的S形函数制作神经网络。虽然人工智能研究人员还使用其他外形类似的函数，但是S函数简单，并且事实上非常常见，因此S函数对我们非常重要。

S函数，有时也称为逻辑函数：

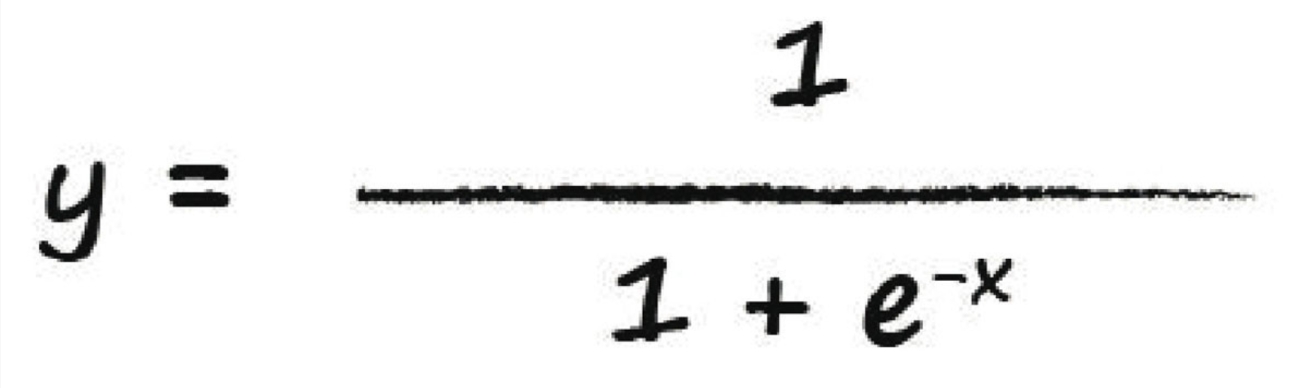
这个表达式乍看来比较可怕，其实也是“纸老虎”。字母e是数学常数2.71828 ……，这是一个非常有趣的数字，出现在各种数学和物理学领域，我使用省略号的原因是，这是一个无限不循环小数。这样的数字有一个奇特的名字—超越数（transcendental number）。这很有趣，很好玩吧，但是出于我们的目的，你可以把它当作2.71828。上面那个看起来有点可怕的函数先对输入x取反，计算出e的-x次方，然后将所得到的结果加1，得到1+e -x；最后，对整个结果取倒数，也就是1除以1+e -x，做为输出值y给出。这就是上面那个看起来有点可怕的函数，它对输入的x进行操作，然后给出输出值y。因此，这没有那么可怕。

出于兴趣，由于任何数的0次方都等于1，因此当x为0时，e -x为1。因此y变成了1/（1+1），为1/2。此时，基本S形函数在y=½时，对y轴进行切分。

我们使用这种S函数，而不使用其他可以用于神经元输出的S形函数，还有另一个非常重要的原因，那就是，这个S函数比起其他S形函数计算起来容易得多，在后面的实践中，我们会看到为什么。

让我们回到神经元，并思考我们如何建模人工神经。

读者要认识到的第一件事情是生物神经元可以接受许多输入，而不仅仅是一个输入。刚才，我们观察了布尔逻辑机器有两个输入，因此，有多个输入的想法并不新鲜，并非不同寻常。

对于所有这些输入，我们该做些什么呢？我们只需对它们进行相加，得到最终总和，作为S函数的输入，然后输出结果。这实际上反映了神经元的工作机制。下图说明了这种组合输入，然后对最终输入总和使用阈值的思路。

如果组合信号不够强大，那么S阈值函数的效果是抑制输出信号。如果总和x足够大，S函数的效果就是激发神经元。有趣的是，如果只有其中一个输入足够大，其他输入都很小，那么这也足够激发神经元。更重要的是，如果其中一些输入，单个而言一般大，但不是非常大，这样由于信号的组合足够大，超过阈值，那么神经元也能激发。这给读者带来了一种直观的感觉，即这些神经元也可以进行一些相对复杂、在某种意义上有点模糊的计算。

树突收集了这些电信号，将其组合形成更强的电信号。如果信号足够强，超过阈值，神经元就会发射信号，沿着轴突，到达终端，将信号传递给下一个神经元的树突。下图显示了使用这种方式连接的若干神经元。

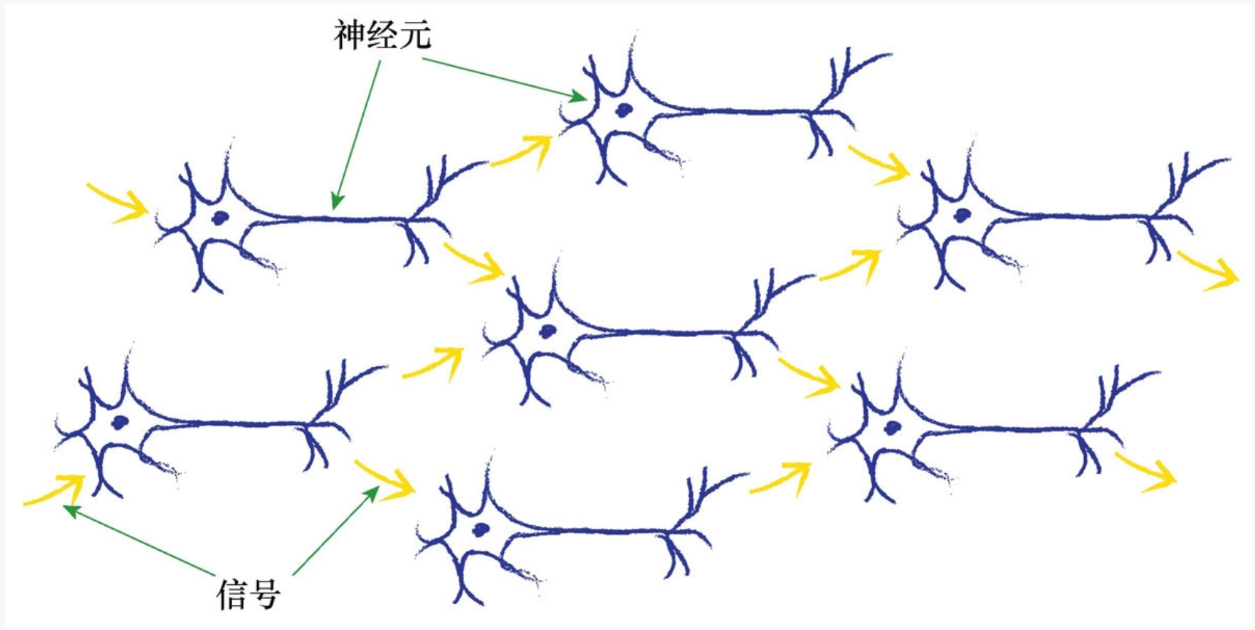
需要注意的一点是，每个神经元接受来自其之前多个神经元的输入，并且如果神经元被激发了，它也同时提供信号给更多的神经元。

将这种自然形式复制到人造模型的一种方法是，构建多层神经元，每一层中的神经元都与在其前后层的神经元互相连接。下图详细描述了这种思想。

你可以看到三层神经元，每一层有三个人工神经元或节点。你还可以看到每个节点都与前一层或后续层的其他每一个节点互相连接。

这真是太棒了！但是，这看起来很酷的体系架构，哪一部分能够执行学习功能呢？针对训练样本，我们应该如何调整做出反应呢？有没有和先前线性分类器中的斜率类似的参数供我们调整呢？

最明显的一点就是调整节点之间的连接强度。在一个节点内，我们可以调整输入的总和或S阈值函数的形状，但是比起简单地调整节点之间的连接强度，调整S阀值函数的形状要相对复杂。

如果相对简单的方法可以工作，那么请坚持这种方法！下图再一次显示了连接的节点，但是这次在每个连接上显示了相关的权重。较小的权重将弱化信号，而较大的权重将放大信号。

此处，我需要解释一下权重符号旁边的有趣小数字（即下标）。简单说来，权重w2,3与前一层节点2传递给下一层的节点3的信号相关联。因此，权重w1,2减小或放大节点1传递给下一层节点2的信号。为了详细说明这种思路，下图突出显示了第一层和第二层之间的两条连接。

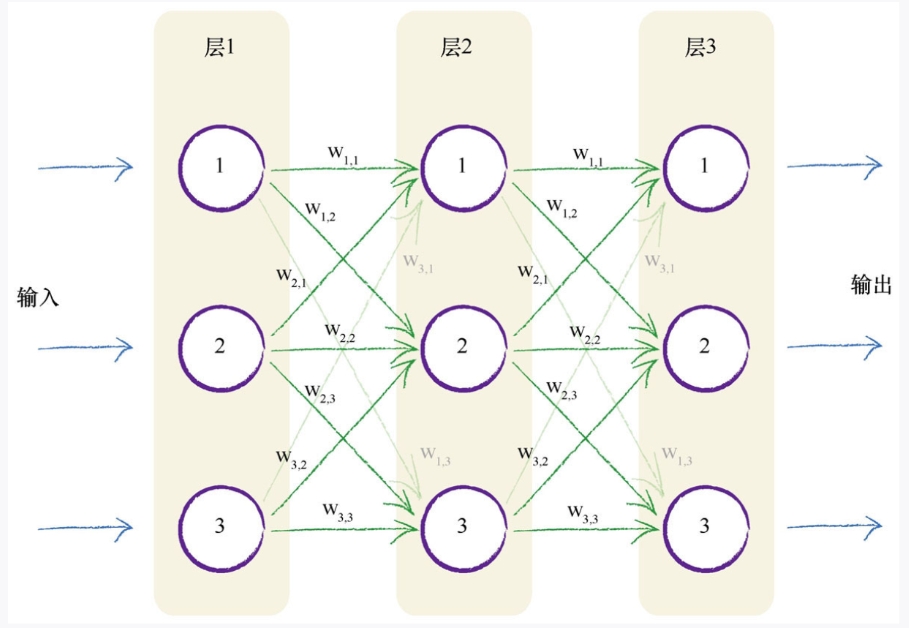
你可能有充分的理由来挑战这种设计，质问为什么必须把前后层的每一个神经元与所有其他层的神经元互相连接，并且你甚至可以提出各种创造性的方式将这些神经元连接起来。我们不采用创造性的方式将神经元连接起来，原因有两点，第一是这种一致的完全连接形式事实上可以相对容易地编码成计算机指令，第二是神经网络的学习过程将会弱化这些实际上不需要的连接（也就是这些连接的权重将趋近于0），因此对于解决特定任务所需最小数量的连接冗余几个连接，也无伤大雅。

说起这个，我们的意思是什么呢？这意味着，随着神经网络学习过程的进行，神经网络通过调整优化网络内部的链接权重改进输出，一些权重可能会变为零或接近于零。零或几乎为零的权重意味着这些链接对网络的贡献为零，因为没有传递信号。零权重意味着信号乘以零，结果得到零，因此这个链接实际上是被断开了。